1LocusSim: SIMULACIÓN DE UN LOCUS CON DERIVA GENÉTICA, MUTACIÓN Y SELECCIÓN

Características
- 1LocusSim es un simulador sencillo y adaptable (apto para móviles) para visualizar el efecto de la deriva genética, la selección y la mutación en la frecuencia alélica.
- Está programado en Python apoyándose en la librería NumPy.
Contacto
Para cualquier duda me puedes contactar
.
Vuelve a AC-R home
Simulación de la deriva genética
Deriva genética
En el simulador el censo de población N se corresponde al censo efectivo Ne siempre y cuando no haya mutación ni selección, pues el apareamiento es al azar y por defecto se permite autofecundación. Las fluctuaciones aleatorias de la frecuencia alélica q se manifestarán en un incremento de la varianza de la frecuencia alélica σ2q entre distintas subpoblaciones o réplicas. Para un mismo número de poblaciones y generaciones veremos que la varianza aumenta más rápidamente si Ne es bajo. Por ejemplo, con 20 poblaciones podemos apreciar en la Figura 1 la comparación entre el caso Ne = 10 y Ne=1000 tras 100 generaciones de evolución.
A Ne = 10 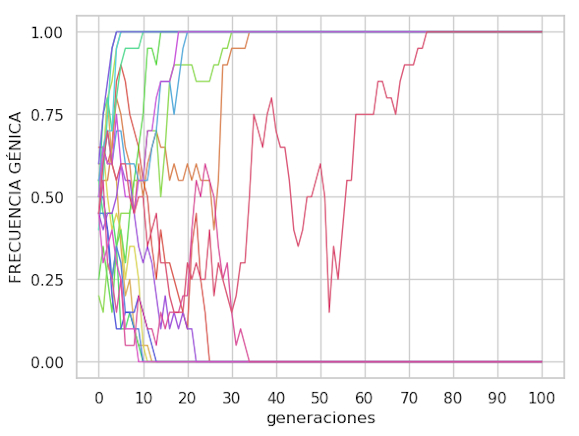

B Ne = 1000 

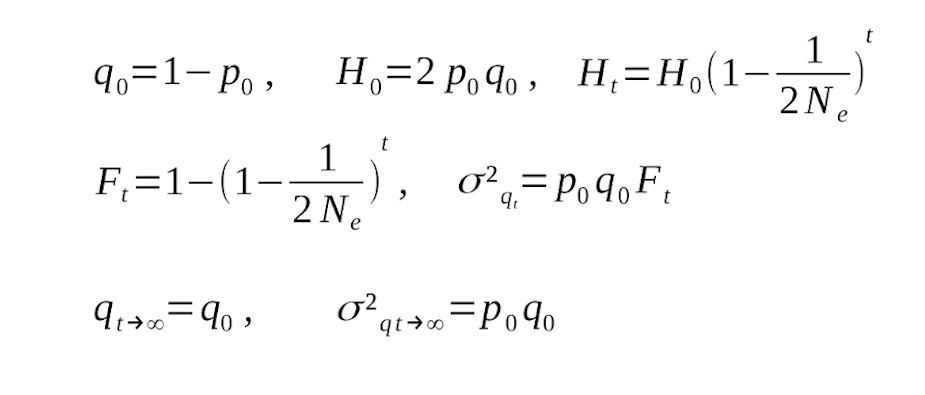
Ejercicios
En la Figura 2 se muestra la relación matemática entre la deriva y la variabilidad genética. Utiliza las fórmulas que ahí aparecen para resolver los siguiente ejercicios.
Ejercicio 1
En el modelo de deriva inicialmente la varianza entre líneas es 0 porque la frecuencia inicial q0 es la misma para todas las poblaciones. En varios experimentos durante 3 generaciones la varianza se incrementó en más de un 20%. La varianza en la tercera generación fue de 0.21. Si la frecuencia alélica inicial era 0.5 y no hay mutación ni selección ¿cuál era el censo efectivo de la población? Compruébalo mediante simulación.
Inicialmente q0=0.5 y en t=3, σ2q3=0.21
entonces 0.21=0.25×F3 y despejando, F3=0.84.
La relación con el censo efectivo es 0.84=1-(1-1/(2Ne))3. Por tanto
(1-1/(2Ne))3=0.16.
Calculando la raíz cúbica a ambos lados de la igualdad y despejando Ne obtenemos
1-1/(2Ne)=0.543 => 0.457=1/(2Ne) => Ne≈1.
Ejercicio 2
Se simularon 100 poblaciones con frecuencia inicial q0=0.5. Tras 5 generaciones la varianza de q fue aproximadamente 0.1. No hay mutación ni selección ¿Dirías que el censo efectivo está en torno a 5 o a 50? Justifica tu respuesta y compruébalo mediante una simulación.
Recordemos que a menor censo efectivo más rápido es el incremento de la varianza. Sabemos que
σ2q5=p0q0F5.
Como p0=q0=0.5 y σ2q5≈0.1
tenemos que 0.1=0.25×F5 y despejando, F5=0.4.
Si fuera Ne=5 entonces F5=1-(1-1/(2Ne))5=1-(1-1/(10))5=0.41.
Si fuera Ne=50 entonces F5=1-(1-1/(2Ne))5=1-(1-1/(100))5=0.05.
Con lo cual parece que el censo efectivo está en torno a 5 y no a 50. Lo cual podemos comprobar fácilmente realizando una simulación con parámetros n=100, q0=0.5, t=5 sin mutación ni selección y probando primero Ne=5 y después Ne=50. Y comprobando en cada caso el valor de la varianza obtenida (esperamos que sea aproximadamente 0.1).
Ejercicio 3
¿Cuál será el número mínimo de generaciones necesarias para que en un conjunto de poblaciones de censo 5, la varianza entre líneas obtenida valga la mitad de la varianza máxima? PISTA: recuerda que la varianza máxima es p0q0.
Si Ne=5 entonces Ft=1-(1-1/10)t=1-0.9t.
Como σ2qt=p0q0Ft
tenemos que
p0q0/2=p0q0Ft
y por tanto Ft=0.5=1-0.9t=>0.9t=0.5.
Tomando logaritmos a ambos lados, t=log(0.5)/log(0.9)=6.6≈7 serán el número mínimo de generaciones necesarias.
A. Carvajal-Rodriguez - Departamento de Bioquímica Genética e Inmunología - Universidad de Vigo.
( Actualizado: Marzo 2023)
