Given an encounter between an i-type female and a j-type male, let the probability of mating to depend on the mutual mating propensity m_ij. Therefore, the mating probability between types i and j is expressed as q'_ij = m_ijq_ij where q_ij is the encounter probability i.e. the product of the population female and male frequencies of each type (q_ij = p_1ixp_2j = (n_1in_2j) / (n₁n₂) and n_1i is the number of females of type i from the total of n₁ females in the population and n_2j is the number of males j from n₂ males in the population). The values m_ij are normalized so that the summatory q'_ij = 1 (Carvajal-Rodriguez 2018).

Therefore, consider a sample of n' matings between different types of females and males. If there are k₁ types of females and k₂ types of males then the total number of possible matings is K = k₁ x k₂. Let have a sample with n'_ij matings of i type female with j type male. If the probability of the mating i x j is q'_ij, the logarithm of the likelihood function of the sample is

where C is the multinomial coefficient which is constant given the mating data. The maximum likelihood estimator (MLE) of the probability of the mating i × j is n'_ij / n' and if we consider the population frequencies q_ij as already known, then the MLE of m_ij corresponds to the Pair Total Index PTI(i,j).

We say this model M_sat is saturated because it has as many parameters as data categories in the sample i.e. it is the most complex model that can be fitted to the available data. Interestingly, it is possible to show that the random mating model M₀ corresponds to M_sat subjected to the following restrictions:

1. Multiplicative effects: m_ij= m_{Fem_ii} × m_{Male_j} for every i,j
2. Equal female marginals: m_{Fem_i} = m_{Fem_j} for every i,j
3. Equal male marginals: m_{Male_i} = m_{Male_j} for every i,j

It is useful to express the random mating model in such a way because we can generate particular models of interest by relaxing some of the conditions.

 

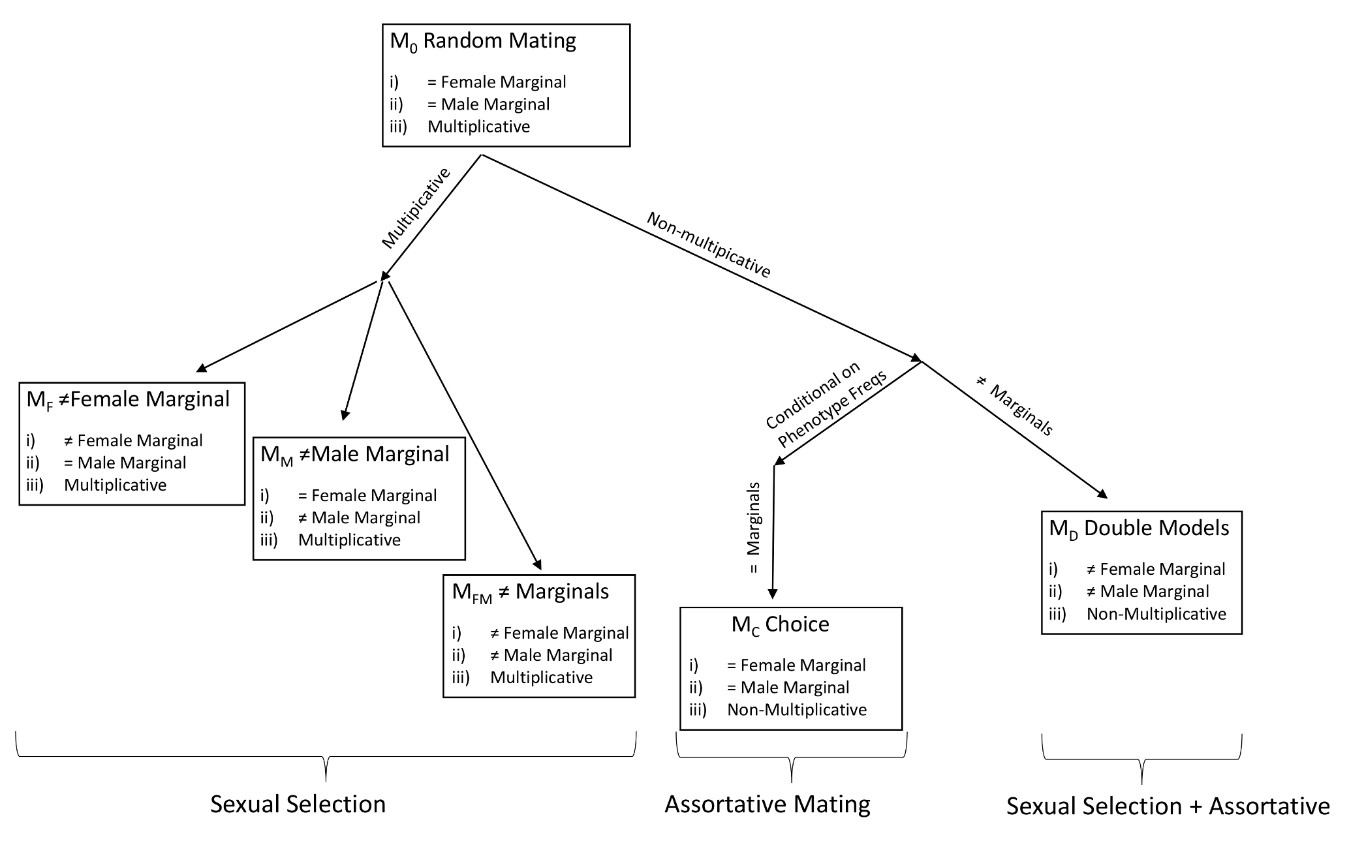
Thus, we can develop a set of hypotheses corresponding to different mate choice and intrasexual competition effects and then using data-based evidence for ranking each hypothesis and perform multi-model-based inference. The QInfoMating program performs this task.